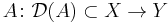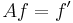Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the spectrum and (with certain assumptions) functional calculus for such operators. Many important linear operators which fail to be bounded turn out to be closed, such as the derivative and a large class of differential operators.
Let 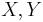 be two Banach spaces. A linear operator
be two Banach spaces. A linear operator
is closed if for every sequence 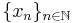 in
in 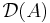 converging to
converging to 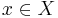 such that
such that  as
as 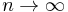 one has
one has 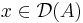 and
and 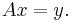 Equivalently,
Equivalently,  is closed if its graph is closed in the direct sum
is closed if its graph is closed in the direct sum 
Given a linear operator  , not necessarily closed, if the closure of its graph in
, not necessarily closed, if the closure of its graph in  happens to be the graph of some operator, that operator is called the closure of
happens to be the graph of some operator, that operator is called the closure of  , and we say that
, and we say that  is closable. Denote the closure of
is closable. Denote the closure of  by
by 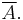 It follows easily that
It follows easily that  is the restriction of
is the restriction of 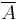 to
to 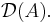
A core of a closable operator is a subset  of
of 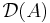 such that the closure of the restriction of
such that the closure of the restriction of  to
to  is
is 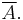
Basic Properties
The following properties are easily checked:
- Any closed linear operator defined on the whole space
 is bounded. This is the closed graph theorem;
is bounded. This is the closed graph theorem; - If
 is closed then
is closed then 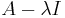 is closed where
is closed where  is a scalar and
is a scalar and  is the identity function;
is the identity function; - If
 is closed, then its kernel (or nullspace) is a closed subspace of
is closed, then its kernel (or nullspace) is a closed subspace of  ;
; - If
 is closed and injective, then its inverse
is closed and injective, then its inverse 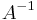 is also closed;
is also closed; - An operator
 admits a closure if and only if for every pair of sequences
admits a closure if and only if for every pair of sequences 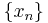 and
and 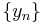 in
in 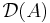 both converging to
both converging to  , such that both
, such that both 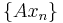 and
and 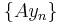 converge, one has
converge, one has 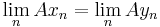 .
.
Example
Consider the derivative operator
where the Banach space X=Y is the space C[a, b] of all continuous functions on an interval [a, b]. If one takes its domain 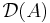 to be
to be ![\mathcal{D}(A)=C^{1}[a, b]](/2012-wikipedia_en_all_nopic_01_2012/I/1027f9a9bc81a5cc9509856095e5fba5.png) , then A is a closed operator, which is not bounded. (Note that one could also set
, then A is a closed operator, which is not bounded. (Note that one could also set 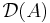 to be the set of all differentiable functions including those with non-continuous derivative. That operator is not closed!)
to be the set of all differentiable functions including those with non-continuous derivative. That operator is not closed!)
If one takes 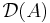 to be instead the set of all infinitely differentiable functions, A will no longer be closed, but it will be closable, with the closure being its extension defined on
to be instead the set of all infinitely differentiable functions, A will no longer be closed, but it will be closable, with the closure being its extension defined on ![C^{1}[a, b]](/2012-wikipedia_en_all_nopic_01_2012/I/1923a9d64e0967b1a44d19438f4e9de4.png) .
.
See also densely defined operator and unbounded operator.
This article incorporates material from Closed operator on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.